Distribution of eddy electric currents in an anisotropic electrically conductive transformer

Anatoly Ashcheulov; Mykola Derevianchuk

doi:10.15222/TKEA2025.3-4.03

Anatoly Ashcheulov Yurii Fedkovych Chernivtsi National University, Ukraine https://orcid.org/0000-0002-3195-6342
Mykola Derevianchuk Yurii Fedkovych Chernivtsi National University, Ukraine https://orcid.org/0000-0001-7218-1451

DOI: https://doi.org/10.15222/TKEA2025.3-4.03

Keywords: electrical conductivity, anisotropy, eddy electric current, transformer, infocommunication system elements, tensor

Abstract

This paper investigates the formation and spatial distribution of eddy electric currents (EEC) within the structure of an anisotropic electrically conductive transformer (AECT), which represents a promising functional component for modern infocommunication systems. The research is based on a mathematical formulation that accounts for the tensor nature of the material’s electrical conductivity and the dependence of current distribution on the anisotropy coefficient K and the rotation angle of the crystallographic axes relative to the laboratory coordinate system γ.

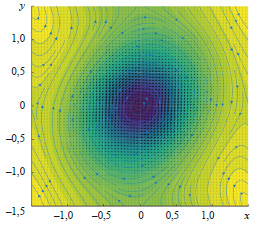
A differential-form equation describing the behavior of eddy currents in a rectangular plate composed of an anisotropic material has been derived. It is shown that this equation exhibits an elliptic character, which significantly influences both the configuration and density of the eddy current distribution. Numerical modeling of current patterns has been performed, followed by visualization in the form of vector field maps for various values of K and angles γ.

Analysis of the simulation results reveals that the anisotropy coefficient governs the geometry of the eddy current loops: for K > 1, the elongation of the elliptical contours occurs along the axis with higher conductivity, while for K < 1, it occurs along the orthogonal axis. The angle γ determines the orientation of the principal axes within the laboratory plane and, consequently, the direction of elongation of the eddy structures. Meanwhile, the rotation direction of the eddy electric currents (CW/CCW) remains constant and is determined by the polarity of the applied voltage.

The practical significance of this study lies in establishing the relationship between anisotropy parameters and thermal losses within the transformer’s volume. It has been found that at higher K values, local losses decrease due to a more uniform current distribution along the major axis, whereas for 0 < K < 1, a more concentrated distribution is formed with intense local heating zones. These findings enable consideration of the anisotropic electrically conductive transformers operational characteristics in the design of telecommunication system components, particularly in power supply and coupling units.

Thus, this work presents, for the first time, a Laplacian-type equation for the distribution of eddy electric currents that incorporates material anisotropy, provides its classification, and demonstrates numerical implementation. The obtained results are of both scientific and practical interest for the development of new high-efficiency components in infocommunication technologies.

References

A. A. Ashcheulov, M. Ya. Derevianchuk, D. A. Lavreniuk, and I. S. Romaniuk, “Electric current transformation by anisotropic electrically conductive medium,” Tekhnologiya i Konstruirovanie v Elektronnoi Apparature, no. 5–6, pp. 28–32, 2020, doi: 10.15222/TKEA2020.5-6.28.

A. A. Ashcheulov, “On energy opportunities in anisotropic bipolar electrically conductive media,” Journal of Thermoelectricity, no. 3, pp. 5–18, 2021, doi: 10.63527/1607-8829-2021-3-5-18.

A. Ashcheulov, M. Derevianchuk, and D. Lavreniuk, “The method of turbulent transformation of energy,” Engineering Reports, 2023, Art. e12620, doi: 10.1002/eng2.12620.

A. A. Ashcheulov, M. Ya. Derevianchuk, D. O. Lavreniuk, and I. S. Romaniuk, “Anisotropic electrically conductive material,” Patent of Ukraine no. 147993, Bull. no. 25, 2021.

A. Ashcheulov, M. Derevianchuk, D. Lavreniuk, and M. Rozhdestvenska, “Thermal losses of an anisotropic electrically conductive transformer,” Security of Infocommunication Systems and Internet of Things, vol. 3, no. 1, p. 01005, 2025, doi: 10.31861/sisiot2025.1.01005.

L. I. Anatychuk, Thermoelectricity, Vol. 1: Physics of Thermoelectricity. Kyiv–Chernivtsi: Institute of Thermoelectricity, 1998.

L. I. Anatychuk, Thermoelectricity, Vol. 2: Thermoelectric Power Converters. Kyiv–Chernivtsi: Institute of Thermoelectricity, 2005.

M. E. Orazem, and B. Tribollet, Electrochemical Impedance Spectroscopy, 2nd ed. Hoboken, NJ: Wiley, 2021.

J. F. Nye, Physical Properties of Crystals: Their Representation by Tensors and Matrices, Oxford: Oxford Univ. Press, 1985.

L. D. Landau, and E. M. Lifshitz, Electrodynamics of Continuous Media. Oxford: Pergamon Press, 1984, 460 p.

S. Tarasovs, and A. Aniskevich, “Identification of the anisotropic thermal conductivity by an inverse solution using the transient plane source method,” Measurement, vol. 206, Article 112252, 2023, doi: 10.1016/j.measurement.2022.112252.

L. C. Evans, Partial Differential Equations, 2nd ed. Providence, RI: American Mathematical Society, 2022, 662 p.

C. R. Harris, K. J. Millman, S. J. van der Walt, et al., “Array programming with NumPy,” Nature, vol. 585, pp. 357–362, 2020, doi: 10.1038/s41586-020-2649-2.

W. McKinney, Python for Data Analysis: Data Wrangling with pandas, NumPy, and Jupyter, 3rd ed., Sebastopol, CA: O’Reilly Media, 2022, 582 p.

J. D. Hunter, “Matplotlib: A 2D Graphics Environment,” Computing in Science and Engineering, vol. 9, no. 3, pp. 90–95, 2007, doi: 10.1109/MCSE.2007.55.

S. Han, and I. Y. Kwak, “Mastering data visualization with Python: practical tips for researchers,” J. Minim. Invasive Surg., vol. 26, no. 4, pp. 167–175, Dec. 2023, doi: 10.7602/jmis.2023.26.4.167.